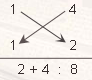matha namo namaha


ŨRDHVA TIRYAGBHYĀM
Urdhva – tiryagbhyam is the general formula applicable to all cases of multiplication and also in the division of a large number by another large number. It means “Vertically and cross wise.”
(a) Multiplication of two 2 digit numbers.
Ex.1:  Find the product 14 X 12
i) The right hand most digit of the multiplicand, the first number (14) i.e., 4 is multiplied by the right hand most digit of the multiplier, the second number (12) i.e., 2. The product 4 X 2 = 8 forms the right hand most part of the answer.
ii) Now, diagonally multiply the first digit of the multiplicand (14) i.e., 4 and second digit of the multiplier (12) i.e., 1 (answer 4 X 1=4); then multiply the second digit of the multiplicand i.e., 1 and first digit of the multiplier i.e., 2 (answer 1 X 2 = 2); add these two i.e., 4 + 2 = 6. It gives the next, i.e., second digit of the answer. Hence second digit of the answer is 6.
iii) Now, multiply the second digit of the multiplicand i.e., 1 and second digit of the multiplier i.e., 1 vertically, i.e., 1 X 1 = 1. It gives the left hand most part of the answer.
Thus the answer is 16 8.
Symbolically we can represent the process as follows :
                         
The symbols are operated from right to left .
      Step i) :
                               
Step ii) :
                          
Step iii) :
                     
      Now in the same process, answer can be written as
                               23
                                    13
                          ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
                          2 : 6 + 3 : 9  =  299      (Recall the 3 steps)
Ex.3
                                    41
                                 X 41
                          ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ 
                          16 : 4 + 4 : 1 = 1681.
What happens when one of the results i.e., either in the last digit or in the middle digit of the result, contains more than 1 digit ? Answer is simple. The right – hand – most digit there of is to be put down there and the preceding, i.e., left –hand –side digit or digits should be carried over to the left and placed under the previous digit or digits of the upper row. The digits carried over may be written as in Ex. 4.
Ex.4:         32 X 24
Step (i) :     2 X 4 = 8
Step (ii) :     3 X 4 = 12; 2 X 2 = 4; 12 + 4 = 16.
Here 6 is to be retained. 1 is to be carried out to left side.
Step (iii) :     3 X 2 = 6. Now the carried over digit 1 of 16 is to be added.
                        i.e., 6 + 1 = 7.
Thus 32 X 24 = 768
We can write it as follows
                                            32
                                            24
                                          ¯¯¯¯
                                           668
                                           1
                                          ¯¯¯¯
                                           768.
Note that the carried over digit from the result (3X4) + (2X2) = 12+4 = 16 i.e., 1 is placed under the previous digit 3 X 2 = 6 and added.
After sufficient practice, you feel no necessity of writing in this way and simply operate or perform mentally.
Ex.5         28 X 35.
Step (i) :     8 X 5 = 40. 0 is retained as the first digit of the answer and 4 is carried   over.

Step (ii) :     2 X 5 = 10; 8 X 3 = 24; 10 + 24 = 34; add the carried over 4 to 34. Now the result is 34 + 4 = 38. Now 8 is retained as the second digit of the answer and 3   is carried over.

Step (iii) :    2 X 3 = 6; add the carried over 3 to 6. The result 6 + 3 = 9 is the third or final digit from right to left of the answer.

Thus 28 X 35 = 980.
Ex.6
                                 48
                                 47
                              ¯¯¯¯¯¯
                               1606
                                 65
                              ¯¯¯¯¯¯¯
                               2256
Step (i):     8 X 7 = 56; 5, the carried over digit is placed below the second digit.

Step (ii):     ( 4 X 7) + (8 X 4) = 28 + 32 = 60; 6, the carried over digit is placed below the third digit.

Step (iii):     Respective digits are added.
Algebraic proof :
    a) Let the two 2 digit numbers be (ax+b) and (cx+d). Note that x = 10. Now consider the product
       (ax + b) (cx + d)  =  ac.x2 + adx + bcx + b.d
                                =  ac.x2 + (ad + bc)x + b.d
Observe that
i) The first term i.e., the coefficient of x2 (i.e., 100, hence the digit in the 100th place) is obtained by vertical multiplication of a and c i.e., the digits in 10th place (coefficient of x) of both the numbers;

ii) The middle term, i.e., the coefficient of x (i.e., digit in the 10th place) is obtained by cross wise multiplication of a and d; and of b and c; and the addition of the two products;

iii) The last (independent of x) term is obtained by vertical multiplication of the independent terms b and d.
b) Consider the multiplication of two 3 digit numbers.
Let the two numbers be (ax2 + bx + c) and (dx2 + ex + f). Note that x=10
Now the product is
                            ax2 + bx + c
                          x dx2 + ex + f
          ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
         ad.x4+bd.x3+cd.x2+ae.x3+be.x2+ce.x+af.x2+bf.x+cf
= ad.x4 + (bd + ae). x3 + (cd + be + af).x2 + (ce + bf)x + cf
Note the following points :
 i)  The coefficient of x4 , i.e., ad is obtained by the vertical multiplication of the first coefficient from the left side :
                       
ii)The coefficient of x3 , i.e., (ae + bd) is obtained by the cross –wise multiplication of the first two coefficients and by the addition of the two products;
                       
iii)  The coefficient of x2 is obtained by the multiplication of the first coefficient of the multiplicand (ax2+bx +c) i.e., a; by the last coefficient of the multiplier (dx2 +ex +f) i.e.,f ; of the middle one i.e., b of the multiplicand by the middle one i.e., e of the multiplier and of the last one i.e., c of the multiplicand by the first one i.e., d of the multiplier and by the addition of all the three products i.e., af + be +cd :
                      
iv) The coefficient of x is obtained by the cross wise multiplication of the second coefficient i.e., b of the multiplicand by the third one i.e., f of the multiplier, and conversely the third coefficient i.e., c of the multiplicand by the second coefficient i.e., e of the multiplier and by addition of the two products, i.e., bf + ce ;
                        
v) And finally the last (independent of x) term is obtained by the vertical multiplication of the last coefficients c and f i.e., cf
                   
Thus the process can be put symbolically as (from left to right)
                  
Consider the following example
                            124 X 132.
Proceeding from right to left
i) 4 X 2 = 8. First digit = 8

ii) (2 X 2) + (3 X 4) = 4 + 12 = 16. The digit 6 is retained and 1 is carried over to left side. Second digit = 6.

iii) (1 X 2) + (2 X 3) + (1 X 4) = 2 + 6 + 4 =12. The carried over 1 of above step is added i.e., 12 + 1 = 13. Now 3 is retained and 1 is carried over to left side. Thus third digit = 3.

iv) ( 1X 3 ) + ( 2 X 1 ) = 3 + 2 = 5. the carried over 1 of above step is added i.e., 5 + 1 = 6 . It is retained. Thus fourth digit = 6

v) ( 1 X 1 ) = 1. As there is no carried over number from the previous step it is retained. Thus fifth digit = 1

                    124 X 132 = 16368.
Let us work another problem by placing the carried over digits under the first row and proceed.
                             234
                               x 316
                               ¯¯¯¯¯¯¯
                                61724
                                1222
                               ¯¯¯¯¯¯¯
                                73944
i) 4 X 6 = 24 : 2, the carried over digit is placed below the second digit.

ii) (3 X 6) + (4 x 1) = 18 + 4 = 22 ; 2, the carried over digit is placed below third digit.

iii) (2 X 6) + (3 X 1) + (4 X 3) = 12 + 3 + 12 = 27 ; 2, the carried over digit is placed below fourth digit.

iv) (2 X 1) + ( 3 X 3) = 2 + 9 = 11; 1, the carried over digit is placed below fifth digit.

v) ( 2 X 3 ) = 6.

vi) Respective digits are added.
Note :
1. We can carry out the multiplication in urdhva - tiryak process from left to right or right to left.

2. The same process can be applied even for numbers having more digits.

3. urdhva –tiryak process of multiplication can be effectively used in multiplication regarding algebraic expressions.
Example 1 : Find the product of (a+2b) and (3a+b).
                   
Example 2 :
                             3a2 + 2a + 4
                          x 2a2 + 5a + 3
                         ¯¯¯¯¯¯¯¯¯¯¯¯¯¯
i)     4 X 3   = 12

ii)   (2 X 3)  +  ( 4 X 5 )  =  6 + 20  = 26   i.e., 26a

iii)  (3 X 3)  + ( 2 X 5 ) +  ( 4 X 2 ) = 9 + 10 + 8 = 27  i.e., 27a2

iv)  (3 X 5)  + ( 2 X 2 ) =  15 + 4  =  19  i.e., 19 a3

v)    3 X 2   =   6     i.e., 6a4
Hence the product is 6a4 + 19a3 + 27a2 + 26a + 12
Example 3 :     Find    (3x2 + 4x + 7) (5x +6)
            Now         3.x2 + 4x + 7
                                0.x2 + 5x + 6
                               ¯¯¯¯¯¯¯¯¯¯¯¯
i) 7 X 6 = 42

ii) (4 X 6) + (7 X 5) = 24 + 35 = 59 i.e., 59x

iii) (3 X 6) + (4 X 5) + (7 X 0) = 18 + 20 + 0 = 38 i.e., 38x2

iv) (3 X 5) + (0 X 4) = 15 + 0 = 15 i.e., 15x3

v) 3 X 0 = 0
Hence the product is 15x3 + 38x2 + 59x + 42
        Find the products using urdhva tiryagbhyam process.

        1) 25 X 16                  2) 32 X 48             3) 56 X 56
          
        4) 137 X 214              5) 321 X 213        6) 452 X 348

        7) (2x + 3y) (4x + 5y)                           8) (5a2 + 1) (3a2 + 4)

        9) (6x2 + 5x + 2 ) (3x2 + 4x +7)         10) (4x2 + 3) (5x + 6)
Urdhva – tiryak in converse for division process:
As per the statement it an used as a simple argumentation for division process particularly in algebra.
Consider the division of (x3 + 5x2 + 3x + 7) by (x – 2) process by converse of urdhva – tiryak :
    i)   x3 divided by x gives                       x2 . x3 + 5x2 + 3x + 7
              It is the first term of the Quotient.    ___________________
                                                                           x – 2
                               Q = x2 + - - - - - - - - - - -
ii)   x2 X – 2 = - 2x2 . But 5x2 in the dividend hints 7x2 more since 7x2 – 2x2 = 5x2 . This ‘more’ can be obtained from the multiplication of x by 7x. Hence second term of Q is 7x.
        x3 + 5x2 + 3x + 7
           ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯   gives Q = x2 + 7x + - - - - - - - -
                      x – 2

iii)We now have – 2 X 7x = -14x. But the 3rd term in the dividend is 3x for which ‘17x more’ is required since 17x – 14x =3x.

Now multiplication of x by 17 gives 17x. Hence third term of quotient is 17

        Thus
                    x3 + 5x2 + 3x + 7
                  _________________    gives Q= x2 + 7x +17
                            x – 2

iv) Now last term of Q, i.e., 17 multiplied by –2 gives 17X–2 = -34 but the relevant term in dividend is 7. So 7 + 34 = 41 ‘more’ is required. As there no more terms left in dividend, 41 remains as the remainder.

             x3 + 5x2 + 3x + 7
            ________________   gives Q= x2 + 7x +17 and R = 41.
                      x – 2
Find the Q and R in the following divisions by using the converse process of urdhva – tiryagbhyam method :

1)  3x2 – x – 6                        2) 16x2 + 24x +9
      ¯¯¯¯¯¯¯¯¯                            ¯¯¯¯¯¯¯¯¯¯¯¯
          3x – 7                                          4x+3

3)  x3+ 2x2 +3x + 5             4) 12x4 – 3x2 – 3x + 12
      ¯¯¯¯¯¯¯¯¯¯¯¯¯¯                ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
              x - 3                                           x2 + 1

Publised by sri  

Labels: